Symmetric Difference of Sets

Symmetric Difference is one of the mathematical operation that can be performed on Sets in Python. Set in Python supports mathematical operations like union, intersection, difference, and symmetric difference, subset and super-set, which helps us to analyze and interpret relationships between sets.

In previous article we learned about difference operation on Sets in Python. In this article, we will learn about symmetric difference operation on Sets in Python.

Table of Contents

In mathematics Set theory, Symmetric Difference provides a unique way to understand the elements which belong exclusively to each of the sets involved. Symmetric Difference of Sets refers to the operation between two sets (Set_1 and Set_2), is a set containing elements that are either in Set_1 or in Set_2 but not in both. In other words, symmetric difference of Sets includes elements that are unique to each set, excluding any shared elements or common elements.

Mathematical Definition

In Mathematics, Symmetric Difference of Sets is denoted by the symbol Δ (Delta) or ⊕ (oplus).

Symmetric Difference can be expressed as: A Δ B = ( A - B ) ∪ ( B - A ), where

A - B represents the difference of sets A and B i.e. set of elements which are present in set A but does not exists in Set B.
B - A represents the difference of sets B and A i.e. set of elements which are present in set B but does not exists in Set A.
∪ denotes the union of two sets.

From the expression, Symmetric Difference can also be defined as the Union of cross difference of two sets A and B. Lets see an example:

A = {10, 20, 30, 40} and B = {30, 40, 50, 60}

The symmetric difference A Δ B: A Δ B = {10, 20, 50, 60}. This is because 10 & 20 are in Set A but not in Set B and 50 & 60 are in Set B but not in Set A.

A = {10, 20, 30, 40}

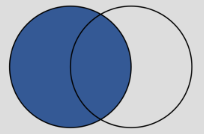
B = {30, 40, 50, 60}

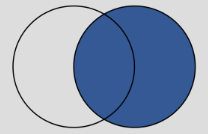
A Δ B ={10,20,50,60}

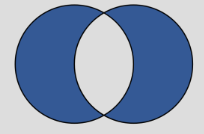
B Δ A ={10,20,50,60}

Properties for Symmetric Difference of Sets

Symmetric difference of two sets A and B (denoted by A Δ B) consists of elements that are in Set A but not in Set B and (union) elements that are in Set B but not in Set A.
Symmetric difference operation between two sets is commutative. Commutative: A Δ B = B Δ A
Symmetric difference operation is also associative. Associative property allows to group sets without affecting the final result. Associative = A Δ ( B Δ C ) = ( A Δ B ) Δ C
Identity: A Δ ∅ = A. It means, symmetric difference between set A and an empty set will result in Set A.
Self inverse: A Δ A = ∅. It means, symmetric difference of set with itself will result in empty set.
Relation to Intersection and Union: Symmetric difference expressed using the union and intersection of sets: A Δ B = ( A ∪ B ) - ( A ∩ B ). This is the difference of union of sets and intersection of sets.

Python provides multiple built-in method to perform Symmetric Difference operation between sets.

Using `symmetric_difference_update()` method

Syntax – set_1.symmetric_difference_update(set_2)
symmetric_difference_update() method takes a single “iterable” as an argument.
symmetric_difference_update() method returns None (which means it does not return any result-set).
Return – set_1.symmetric_difference_update(set_2) operation will update the set_1 with symmetric difference of given sets.

# using symmetric_difference_update() method
print("symmetric_difference_update() method")

set_1 = {'Python','AWS','ML','Java','Azure'}
set_2 = {'PHP','UI','MongoDB','Java','Azure'}

difference_set12 = set_1.symmetric_difference_update(set_2)        # symmetric difference

print(set_1)
print(set_2)
print(difference_set12)

We have defined two sets referenced by variables ‘set_1’ and ‘set_2’. We are using built-in symmetric_difference_update() method on first set ‘set_1’ and second set is passed as an argument to symmetric_difference_update() method. symmetric_difference_update() method will return None (i.e. it will not return any result-set).

‘set_1’ will be updated with all elements in both sets ‘set_1’ and ‘set_2’ excluding the elements which are common in both the sets. Returned value assigned to a variable ‘difference_set12’ should be None. At end we are printing all the sets.

Program Output

symmetric_difference_update() method
{'AWS', 'PHP', 'UI', 'Python', 'MongoDB', 'ML'}            # set_1 updated with symmetric difference of elements
{'PHP', 'Java', 'UI', 'Azure', 'MongoDB'}
None                       # None returned

From the program output, ‘set_1’ elements are updated with the result of symmetric difference operation. Now ‘set_1’ contains all elements which were in set_1 and set_2 excluding the elements which were common in both sets. symmetric_difference_update() method return None.

Using `symmetric_difference()` method

Syntax – set_1.symmetric_difference(set_2), will return the result-set with all elements from both sets (set_1 and set_2) excluding the elements which were common in both sets.
symmetric_difference is a commutative operation. i.e.
set_2.symmetric_difference(set_1) = set_1.symmetric_difference(set_2)

# using symmetric_difference() method
print("symmetric_difference() method")

set_1 = {'Python', 'AWS', 'ML', 'Java', 'Azure'}
set_2 = {'PHP', 'UI', 'MongoDB', 'Java', 'Azure'}

difference_set12 = set_1.symmetric_difference(set_2)           # set_1 symmetric difference set_2
difference_set21 = set_2.symmetric_difference(set_1)           # set_2 symmetric difference set_1

print(set_1)
print(set_2)
print(difference_set12)
print(difference_set21)

In this program, we have defined two sets referenced by variables ‘set_1’ and ‘set_2’. We are using built-in symmetric_difference () method on first set ‘set_1 and second set ‘set_2’ is passed as an argument to symmetric_difference () method.

Program Output

symmetric_difference() method
{'Python', 'Java', 'ML', 'Azure', 'AWS'}
{'UI', 'Java', 'MongoDB', 'Azure', 'PHP'}
{'UI', 'MongoDB', 'Python', 'ML', 'AWS', 'PHP'}    # result-set of set_1.symmetric_difference(set_2)
{'MongoDB', 'Python', 'UI', 'ML', 'AWS', 'PHP'}    # result-set of set_2.symmetric_difference(set_1)

From the program output, there is no change in the elements of ‘set_1’ and ‘set_2’. After the symmetric difference operation, we got new result sets for both operations. Result set contains all elements from both sets (set_1 and set_2) excluding the elements which were common in both sets.

Using `^` operator

Syntax – symmetric_difference = set_1 ^ set_2

# using ^ operator
print("using ^ operator")

set_1 = {'Python','AWS','ML','Java','Azure'}
set_2 = {'PHP','UI','MongoDB','Java','Azure'}

difference_set12 = set_1 ^ set_2          # set_1 symmetric difference set_2
difference_set21 = set_2 ^ set_1          # set_2 symmetric difference set_1

print(set_1)
print(set_2)
print(difference_set12)
print(difference_set21)

In this program, we are using ^ operator to calculate the symmetric difference.

Program Output

using ^ operator
{'Python', 'Java', 'Azure', 'ML', 'AWS'}
{'Java', 'Azure', 'UI', 'MongoDB', 'PHP'}
{'AWS', 'Python', 'UI', 'ML', 'MongoDB', 'PHP'}
{'MongoDB', 'Python', 'UI', 'ML', 'AWS', 'PHP'}

Summary

In this article we learn about various symmetric difference operation on Sets. Following scenarios were explored:

Symmetric Difference of Sets

Code – Github Repository

All code snippets and programs for this article and for Python tutorial, can be accessed from Github repository – Comments and Docstring in Python.

Python Topics

Interview Questions & Answers

Q: What is the time complexity for symmetric difference of two sets?

Time complexity to find the symmetric difference of two sets in Python is O(min(len(A), len(B))). Symmetric difference has to iterate over the smaller set (out of the two sets) to check for elements that are not in the intersection.

Symmetric difference is equivalent to Union of sets – intersection of sets.

Q: What are the real-world use cases for the symmetric difference of sets?

Symmetric difference can be useful in various real-world scenarios:

Surveys or Polls – Compare responses from different groups to identify unique responses, excluding the common response.
Data Comparison – Compare two datasets to find discrepancies, example – find items that exist in one dataset but not the other.
Version Control – In software development, to find changes that are unique to different branches (i.e., changes that haven’t been merged into a common branch).

Q: What happens if the two sets are the same when calculating the symmetric difference?

If the two sets are identical, their symmetric difference will be an empty set. Since, there will be no unique element in either of the two sets.

set_1 = {15, 28, 43}
set_2 = {15, 28, 43}
symmetric_difference_set12 = set_1 ^ set_2
print(symmetric_difference_set12)  # Elements after symmetric difference => set() or {}

Q: How to find the symmetric difference of more than two sets in Python?

Syntax – symmetric_difference = set_1 ^ set_2 ^ set_3

Q: What are possible errors when working with the symmetric difference of sets?

Mutable elements – Since sets are mutable, we should be careful not to modify a set during iteration or during symmetric difference operations. This can lead to unexpected results.
Non-hashable elements – Sets in Python only allow hashable (like string, tuple, numbers etc.) elements. Set with non-hashable types like lists or dictionaries will raise a TypeError.

Q: Write a program to find the symmetric difference between two lists, preserve the order of elements from the original lists?

def ordered_symmetric_difference(list_1, list_2):
    list_symmetric_difference = []
    for element in list_1:
        if element not in list_2:
            list_symmetric_difference.append(element)
    for element in list_2:
        if element not in list_1:
            list_symmetric_difference.append(element)
    return list_symmetric_difference

# Example usage:
list_1 = [21, 42, 53]
list_2 = [53, 64, 85]
print(ordered_symmetric_difference(list_1, list_2))
# symmetric difference list => [21, 42, 64, 85]

ordered_symmetric_difference(list_1, list_2) function ensures that the order of elements in the symmetric difference remains same as the order given in the original lists.

Symmetric Difference of Sets – Python