NumPy is a powerful Python library for numerical computing, and np.logspace() is one of the powerful function to create array of evenly spaced numbers on logarithmic scale.
In previous tutorials, we learned about Key Features of NumPy Arrays in Python. This tutorial will provide a step-by-step guide to understand how to use np.logspace() effectively, with examples.
np.logspace() to Create Array of Evenly Spaced Numbers on Logarithmic Scale
np.logspace() is a powerful function in NumPy that generates an array of numbers that are evenly spaced on a logarithmic scale. This is particularly useful when you want to create sequences of values over several orders of magnitude, such as in scientific simulations, logarithmic plots, or for applying algorithms that operate over logarithmic ranges.
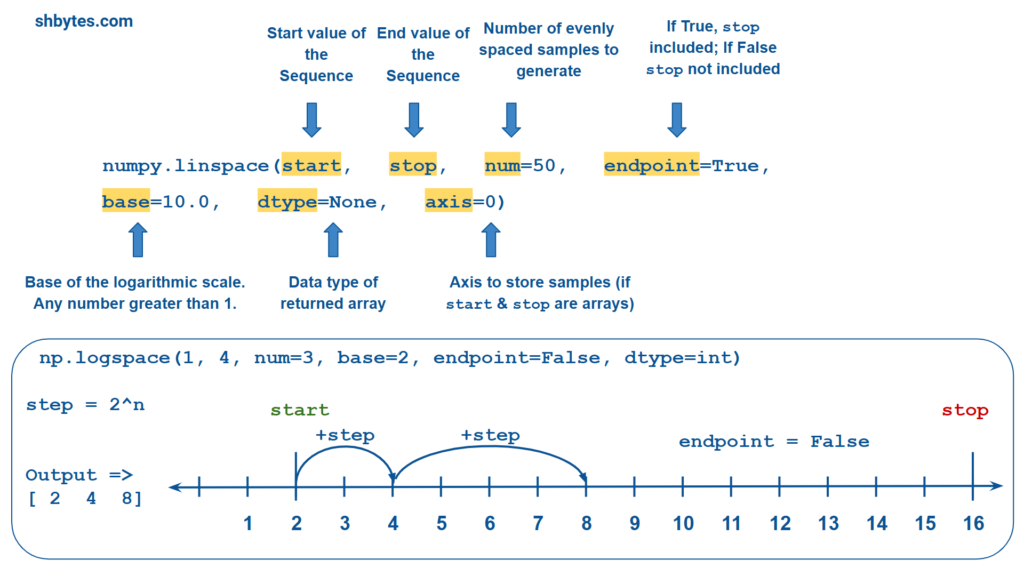
Syntax => np.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None, axis=0)
np.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None, axis=0)start(required) – This is the starting value of the exponent (basebase). This value can be of float or integer. This defines the exponent of the base at the beginning of the range i.ebasestartstop(required) – This is the stopping value of the exponent (basebase). This value can be of float or integer. This defines the exponent of the base at the end of the range i.ebasestopnum(optional) – The number of evenly spaced samples to generate. This defines how many points will be generated in the interval betweenstartandstop. This value can be of positive integer. Default is 50.endpoint(optional) – This is of bool data-type. IfTrue(default),stopis the last value in the sequence. IfFalse, the sequence will end before thestopvalue, i.e., the last point will be just beforebase**stop.base– This is the base of the logarithmic scale. It can be any number greater than 1 (e.g., 2.0, 10.0, etc.). Default is 10.dtype(optional) – This is the data-type of the output array. IfNone(default), it is inferred from the input values.axis(optional) – This is the axis in the result along which thelogspaceis computed. Default is 0. This is of int data-type. This is more relevant when creating multi-dimensional arrays.
How logspace() Function Works
The main idea behind np.logspace() is to compute a series of numbers that are spaced according to the logarithmic scale, rather than linearly. For the given base, the function generates numbers of the form:
base^start,base^(start + step),base^(start + 2 * step), ………,base^stop
For example, if the base is 10 (default), the function generates numbers of the form:
10^start,10^(start + step),10^(start + 2 * step), ………,10^stop
The step is determined by the number of points (num) you want in the range between start and stop. The values are spaced in such a way that the ratio of successive values remains constant.
How Step Size is Calculated for np.logspace() Function
np.logspace(start, stop, num, endpoint) => This function creates a series of numbers that are spaced according to the logarithmic scale, rather than linearly. This logarithmic scale computation of numbers is done based on step size. Step Size Calculation for np.logspace() is done based on a condition.
endpoint=True => The last value in the range will be exactly equal to base^stop value. The step size will be calculated as (stop - start), and dividing it into num - 1 equal intervals (because the last point is already included). => Step Size Calculation (endpoint=True) = (stop - start)/(num - 1)
- Example:
np.logspace(1, 3, num=10, endpoint=True) - The last value in this range will be exactly equal to 10^3.
- Step Size = (3 – 1)/(10 – 1) = 2/9 = 0.222222
- Array =>
10^1,10^(1 + 0.222222),10^(1 + 2 * 0.222222), ………,10^3 - Output Array =>
[ 10. 16.68100537 27.82559402 46.41588834 77.42636827 129.1549665 215.443469 359.38136638 599.48425032 1000. ]
endpoint=False => The last value in the range will exclude the base^stop(stop - start), and dividing it into num equal intervals (because the last point is excluded). => Step Size Calculation (endpoint=False) = (stop - start)/(num)
- Example:
np.logspace(1, 3, num=10, endpoint=False - The last value in this range will exclude value 10^3.
- Step Size = (3 – 1)/(10) = 2/10 = 0.2
- Array =>
10^1,10^(1 + step),10^(start + 2 * step), ………,10^(start + (num - 1) * step) - Last number of array = 10^(1 + 9 * 0.2) = 10^2.8 =
630.95734448 - Output Array =>
[ 10. 15.84893192 25.11886432 39.81071706 63.09573445 158.48931925 251.18864315 398.10717055 630.95734448]
- Step Size Calculation for
endpoint=True=(stop - start)/(num - 1) - Step Size Calculation for
endpoint=False=(stop - start)/(num)
np.logspace() to Create Array with Default Parameters
import numpy as np
# np.logspace() - Create an array from 10^1 to 10^3 (i.e., from 10 to 1000) with Default Parameters
logspace_array_1 = np.logspace(1, 3) # Generate 50 points for base 10 start from 1 to 3
print(logspace_array_1)
# Output
# [ 10. 10.98541142 12.06792641 13.25711366 14.56348478
# 15.9985872 17.57510625 19.30697729 21.20950888 23.29951811
# 25.59547923 28.11768698 30.88843596 33.93221772 37.2759372
# 40.94915062 44.98432669 49.41713361 54.28675439 59.63623317
# 65.51285569 71.9685673 79.06043211 86.85113738 95.40954763
# 104.81131342 115.13953993 126.48552169 138.94954944 152.64179672
# 167.68329368 184.20699693 202.35896477 222.29964825 244.20530945
# 268.26957953 294.70517026 323.74575428 355.64803062 390.69399371
# 429.19342601 471.48663635 517.94746792 568.9866029 625.05519253
# 686.648845 754.31200634 828.64277285 910.29817799 1000. ]In this program, np.logspace(1, 3) will generate num 50 points (default) for base 10 (default) start from 1 to 3.
- First calculate the step size => (3 – 1)/49 = 0.0408163265
- First number in array => 101 = 10
- Second number in array => 10(1+0.0408163265) = 10.98541142
- Third number in array => 10(1+ 2 * 0.0408163265) = 12.06792641
- So on, all the numbers of the array are calculated upto the last number 103 => 1000
- Default data-type of numbers is float.
np.logspace() – Create Array with Specified Number of Points (num)
import numpy as np
logspace_array_2 = np.logspace(0, 3, num=10) # Generate 10 points from 10^0 to 10^3
print(logspace_array_2)
# Output => [ 1. 2.15443469 4.64158883 10. 21.5443469
# 46.41588834 100. 215.443469 464.15888336 1000. ]
logspace_array_3 = np.logspace(0, 3, num=-10) # Negative value for num
print(logspace_array_3)
# Output => ValueError: Number of samples, -10, must be non-negative.np.logspace(0, 3, num=10)=> Thenumparameter controls how many points we need that are evenly spaced on a logarithmic scale. Here, we requestednum(10) points, which gives an array of 10 values. Theendpoint=True(default) option means that 10^3 is included as the last value.np.linspace(0, 3, num=-10)=> In this case, we have defined negative value tonum(-10). This will raise an errorValueError: Number of samples, -10, must be non-negative.
np.logspace() – Create Array using a Different Base
import numpy as np
# np.logspace() - Create an array from 2^1 to 2^10 with base=2
logspace_array_4 = np.logspace(1, 10, num=10, base=2)
print(logspace_array_4)
# Output => [ 2. 4. 8. 16. 32. 64. 128. 256. 512. 1024.]
# np.logspace() - Create an array from 3^1 to 3^7 with base=3
logspace_array_5 = np.logspace(1, 7, num=7, base=3)
print(logspace_array_5)
# Output => [ 3. 9. 27. 81. 243. 729. 2187.]np.logspace(1, 10, num=10, base=2)=>base=2means that the values will be spaced logarithmically with base 2, starting from 21=2 and ending at 210=1024. The sequence will be[21, 22, 23, …, 210], with 10 values.np.logspace(1, 7, num=7, base=3)=>base=3means that the values will be spaced logarithmically with base 3, starting from 31=3 and ending at 37=2187. The sequence will be[31, 32, 33, …, 27], with 7 values.
np.logspace() – Create Array Excluding the stop Value using endpoint=False
import numpy as np
logspace_array_6 = np.logspace(1, 10, num=10, base=2) # Generate 10 points for base 2 start from 1 to 10
print(logspace_array_6)
# Output => [ 2. 4. 8. 16. 32. 64. 128. 256. 512. 1024.]
logspace_array_7 = np.logspace(1, 10, num=10, base=2, endpoint=False)
print(logspace_array_7)
# Output => [ 2. 3.73213197 6.96440451 12.99603834 24.25146506
# 45.254834 84.44850629 157.58648491 294.06677888 548.74801282]endpoint=Trueensures that the last value in the array will bebase^stop. This array will have 10 values spaced logarithmically with base 2. Step size will be equal to (10-1)/(10-1) = 1. Output Array =>[21, 22, 23, …, 210], with 10 values.endpoint=Falseensures that the last value in the array will not bebase^stop(210in this case). The values will still start at 21 but will not reach 210. The array will have 10 values spaced logarithmically with base 2. Step size will be equal to (10-1)/(10) = 0.9. Output Array =>[21, 21.9, 22.8, …, 29.1]
np.logspace() – Specify a Different Data Type (dtype)
import numpy as np
logspace_array_8 = np.logspace(0, 5, num=6, dtype=str) # Array with string data-type
print("String Array:", logspace_array_8)
# Output => String Array: ['1.0' '10.0' '100.0' '1000.0' '10000.0' '100000.0']
logspace_array_9 = np.logspace(0, 5, num=6, dtype=bool) # Array with boolean data-type
print("Boolean Array:", logspace_array_9)
# Output => Boolean Array: [ True True True True True True]
logspace_array_10 = np.logspace(0, 5, num=6, base=2, dtype=complex) # Array with complex data-type
print("Complex Array:", logspace_array_10)
# Output => Complex Array: [ 1.+0.j 2.+0.j 4.+0.j 8.+0.j 16.+0.j 32.+0.j]
logspace_array_11 = np.logspace(0, 5, num=6, dtype=int) # Array with integer data-type
print("Integer Array:", logspace_array_11)
# Output => Integer Array: [ 1 10 100 1000 10000 100000]The dtype argument forces the array to store numbers in given data-type, even though the numbers in the sequence are floa by default.
np.logspace(0, 5, num=6, dtype=str)=> Returns an array with string data-type elements =>['1.0' '10.0' '100.0' '1000.0' '10000.0' '100000.0']np.logspace(0, 5, num=6, dtype=bool)=> Returns an array with boolean data-type elements. Boolean isFalsefor number 0 andTruefor non-zero numbers. =>[ True True True True True True]np.logspace(0, 5, num=6, base=2, dtype=complex)=> Returns an array with complex data-type elements. Number value is real part of complex and imaginary part is 0 =>[ 1.+0.j 2.+0.j 4.+0.j 8.+0.j 16.+0.j 32.+0.j]np.logspace(0, 5, num=6, dtype=int)=> Returns an array with integer data-type elements. The numbers generated will be integers, so any fractional values will be truncated. =>[ 1 10 100 1000 10000 100000]
Create Array in Descending Order using np.logspace()
We can create array in descending order using np.logspace() function.
- If
start < stop=> Array elements will be in ascending order - if
start = stop=> Array with constant elements - If
start > stop=> Array elements will be in descending order
import numpy as np
logspace_array_12 = np.logspace(-3, 2, num=6, base=2) # Array start=-3 (negative) and stop=2 (positive)
print("Array:", logspace_array_12)
# Output => Array: [0.125 0.25 0.5 1. 2. 4. ] (elements in ascending order)
logspace_array_13 = np.logspace(-8, -3, num=6, base=2) # Array start=-8 (negative) and stop=-3 (negative)
print("Array:", logspace_array_13)
# Output => Array: [0.00390625 0.0078125 0.015625 0.03125 0.0625 0.125 ] (elements in ascending order)
logspace_array_14 = np.logspace(2, -3, num=6, base=2) # Array start=2 (positive) and stop=-3 (negative)
print("Array:", logspace_array_14)
# Output => Array: [4. 2. 1. 0.5 0.25 0.125] (elements in descending order)
logspace_array_15 = np.logspace(3, 3, num=6, base=4) # Array start = stop = 3
print("Array:", logspace_array_15)
# Output => Array: [64. 64. 64. 64. 64. 64.]In this example, we will see how array elements can be in ascending or descending order based on positive and negative value for start and stop attributes.
np.logspace(-3, 2, num=6, base=2)=>start(negative) is less thanstop(positive) => Array elements in ascending order =>[0.125 0.25 0.5 1. 2. 4. ]np.logspace(-8, -3, num=6, base=2)=>start(negative) is less thanstop(negative) => Array elements in ascending order =>[0.00390625 0.0078125 0.015625 0.03125 0.0625 0.125 ]np.logspace(2, -3, num=6, base=2)=>start(positive) is greater thanstop(negative) => Array elements in descending order =>[4. 2. 1. 0.5 0.25 0.125]np.logspace(3, 3, num=6, base=4)=> In this casestartis equal tostop=> Array will be of constant values =>[64. 64. 64. 64. 64. 64.]
N-Dimensional Array using np.logspace()
import numpy as np
logspace_array_16 = np.logspace(1, 3, 6, base=10).reshape(2, 3) # Create a 2-D array (e.g., 2x3 array)
print(logspace_array_16)
# Output => [[ 10. 25.11886432 63.09573445]
# [ 158.48931925 398.10717055 1000. ]]
logspace_array_17 = np.logspace(1, 4, 24, base=2).reshape(2, 3, 4) # Create a 3-D array (e.g., 2x3x4 array)
print(logspace_array_17)
# Output => [[[ 2. 2.18924707 2.39640137 2.62315735]
# [ 2.87136977 3.14306893 3.44047723 3.76602735]
# [ 4.12238218 4.51245656 4.93944116 5.40682855]]
#
# [[ 5.91844179 6.47846568 7.09148101 7.76250202]
# [ 8.49701741 9.30103525 10.1811321 11.14450682]
# [12.19903947 13.35335573 14.61689747 16. ]]]np.logspace(1, 3, 6, base=10).reshape(2, 3)=> This creates a 2-D array where the values are logarithmically spaced between 101=10 and 103=1000. We can change the shape or the parameters to suit your needs.np.logspace(1, 4, 24, base=2).reshape(2, 3, 4)=> This creates a 3-D array where the values are logarithmically spaced between 21=2 and 24=16.
Conclusion
In conclusion, the np.logspace() function in NumPy is a powerful tool for generating arrays of numbers spaced evenly on a logarithmic scale. This tutorial covered the essential aspects of np.logspace(), including its basic usage, how it calculates step sizes, and how it can be customized to suit various needs. You can create arrays with a default number of points, specify the number of elements, and even work with different bases.
Additionally, we explored how to exclude the stop value, specify a custom data type, reverse the order of the array, and generate multi-dimensional arrays. Whether you’re working with scientific data or need logarithmic spacing for machine learning or data visualization tasks, np.logspace() provides a flexible and efficient way to create and manipulate arrays on a logarithmic scale.
np.logspace() function in NumPy is useful for generating ranges for algorithms that deal with exponential or logarithmic growth. We can use this function for plotting graphs where the x-axis or y-axis uses a logarithmic scale (e.g., in frequency or time) or in histograms or binned data where you want to group data in logarithmic bins.
Code snippets and programs related to np.logspace(): Create Array of Evenly Spaced Numbers on Logarithmic Scale, can be accessed from GitHub Repository. This GitHub repository all contains programs related to other topics in NumPy tutorial.
Related Topics
- Introduction to NumPy: Core Features and Importance in different FieldsIntroduction to NumPy NumPy stands for Numerical Python. It is an open-source Python library, which is predominantly mostly used for numerical computations in Python. It provides mathematical functions applicable to work with multi-dimensional arrays and matrices. It is a powerful tool to handle large data structures and allows performing complex arithmetic calculations. It has built-in computational features…
- How to Install NumPy on Windows, Linux and Mac: step-by-step guideWe can install NumPy on all major operating systems such as Windows, Linux and macOS. NumPy installation process is very simple and can be done using pip, which is the Python package installer. Here are the steps to install NumPy on Windows, Linux and Mac operating systems. Install NumPy on Windows, Linux and Mac Prerequisites…
- NumPy Array in Python: First Step into Numerical PythonNumPy array in Python are basic entities for numerical computations. They originate from the NumPy library, an essential package in Python for scientific computing. A NumPy array also termed as ndarray, is highly efficient and an object of multi-dimensional array (N-dimensional array), which provides the base functions of numerical operations. Being NumPy Arrays an essential…
- numpy.array(): Create NumPy Arrays using Lists, Tuples and Arrays (with Example Programs)NumPy (Numerical Python) is one of the most powerful libraries for numerical computations, data manipulation, and analysis in Python. At the core of NumPy is the ndarray, a multi-dimensional or N-dimensional array that allows to store and manipulate large datasets efficiently. NumPy provides several ways to create arrays, from simple ones to more complex multi-dimensional…
- Create Arrays with Predefined Values using np.zeros(), np.ones(), np.full() and np.empty()Create Arrays with Predefined Values NumPy library provides various functions to create arrays with predefined values. While creating an array, these NumPy functions helps to initialize the arrays with initial values. In last tutorial, we learned about Key Features of NumPy Arrays in Python. In this article, we will learn about 4 functions to create…
