NumPy (Numerical Python) is a popular Python library used for numerical and scientific computing. It provides a powerful N-dimensional array object called ndarray, which can be used to store and manipulate large datasets efficiently. While NumPy arrays are general-purpose containers for data, the concept of a matrix is often needed when performing operations related to linear algebra, such as matrix multiplication, transposition, and finding determinants.
In previous articles, we learned about NumPy Arrays and How to create NumPy Arrays using Lists or Tuples or using different methods like np.arange(), np.linspace() and np.logspace(). In this article, we will learn about:
- Introduction to NumPy Matrix
- NumPy Array vs NumPy Matrix will cover the differences and similarities between the two
Introduction to NumPy Matrix
In NumPy, the matrix class was specifically designed to handle 2-D arrays (matrices) and provides a set of matrix-specific operations. However, it is now recommended to use ndarray (2-D arrays) for most tasks because ndarray offers more flexibility, and matrix is somewhat limited in its functionality.
Despite that, understanding how to work with matrices in NumPy is crucial when performing linear algebra tasks or when you are working with mathematical computations that require matrix manipulations.
What is Matrix in Mathematics
In Mathematics, a matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. It is a mathematical structure that is used in various fields like algebra, computer science, physics, economics, and engineering. Each element in the matrix is called a matrix entry or element.
Key Points about Matrices
- Dimensions – A matrix is often described by its dimensions, which are given in the form m × n, where m is the number of rows and n is the number of columns. For example, a matrix with 3 rows and 2 columns is a 3 × 2 matrix.
- Notation – A matrix is typically denoted by an uppercase letter, such as A or B. The element at the intersection of the $i$-th row and $j$-th column is often written as $a_{ij}$, where $i$ and $j$ are the row and column indices.
Example of a 2 × 3 Matrix: $A_{2\text{x}3} = \begin{pmatrix}12 & 22 & 32 \\10 & 20 & 30\end{pmatrix}$; This is a matrix with 2 rows and 3 columns.
Types of Matrices
Square Matrix – A matrix with the same number of rows and columns (e.g., a 3 × 3 matrix). Example: $A_{3\text{x}3} = \begin{pmatrix}12 & 22 & 32 \\10 & 20 & 30 \\8 & 15 & 25\end{pmatrix}$; This is a matrix with 3 rows and 3 columns.
Row Matrix – A matrix with only one row (e.g., 1 × n matrix). Example: $A_{1\text{x}4} = \begin{pmatrix}12 & 22 & 32 & 42\end{pmatrix}$; This is a matrix with 1 row and 4 columns.
Column Matrix – A matrix with only one column (e.g., m × 1 matrix). Example: $A_{4\text{x}1} = \begin{pmatrix}12 \\ 22 \\ 32 \\ 42\end{pmatrix}$; This is a matrix with 4 rows and 1 column.
Zero Matrix – A matrix in which all elements are zero. Example: $A_{2\text{x}3} = \begin{pmatrix}0 & 0 & 0 \\0 & 0 & 0\end{pmatrix}$; This is a matrix with 2 rows and 3 columns with all elements are zero.
Identity Matrix – A square matrix with ones on the diagonal and zeros elsewhere. Example: $A_{3\text{x}3} = \begin{pmatrix}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{pmatrix}$; This is a square matrix with 3 rows and 3 columns with ones on the diagonal and zeros elsewhere.
Matrix Operations
- Addition – Matrices of the same dimensions can be added by adding their corresponding elements.
- Multiplication – Matrices can be multiplied, but the number of columns in the first matrix must match the number of rows in the second matrix.
- Transpose – The transpose of a matrix is formed by swapping its rows and columns.
- Determinant – A scalar value that can be computed from a square matrix, used in various computations like solving systems of linear equations.
- Inverse – The inverse of a matrix, if it exists, is a matrix that, when multiplied by the original matrix, results in the identity matrix.
Matrices are powerful tools used for solving systems of linear equations, transformations in computer graphics, and representing data structures in machine learning, among many other applications.
What is a NumPy Matrix?
A NumPy matrix is a 2-D array, a rectangular grid of numbers organized in rows and columns. In NumPy, the matrix class is a specialized 2-D ndarray object, and it enforces a stricter 2-D structure, meaning it only supports two-dimensional arrays. NumPy library provides additional methods specifically designed for matrix operations.
How to Create NumPy Matrix
There are two main ways to create a matrix in NumPy.
Create NumPy Matrix using numpy.matrix()
This method creates a matrix object. It’s less commonly used today, as numpy.ndarray is preferred, but it’s still part of NumPy.
import numpy as np
M = np.matrix([[16, 26], [38, 42]]) # Create a 2x2 matrix
print(M)
# Output => [[16 26] [38 42]]Create NumPy Matrix using numpy.array()
Most of the time, you would use numpy.array() to create a 2D array that can act as a matrix. The key difference between an ndarray and a matrix is that an ndarray can be of any number of dimensions, while a matrix is strictly 2D.
import numpy as np
A = np.array([[16, 26], [38, 42]]) # Create a 2x2 ndarray (which can be treated as a matrix)
print(A)
# Output => [[16 26] [38 42]]NumPy Array vs NumPy Matrix
Both NumPy arrays (ndarray) and NumPy matrices (matrix) are used to represent multi-dimensional data, but there are key differences that influence their functional behavior and operations performed, particularly in terms of matrix operations and dimensionality. Let’s explore these differences in greater detail.
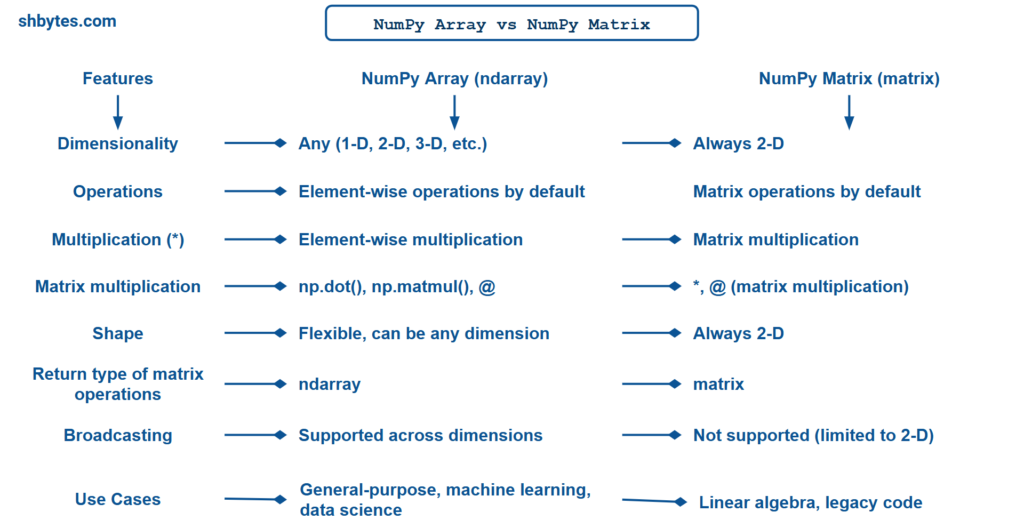
1. Dimensionality
NumPy Array (ndarray) | NumPy Matrix (matrix) |
|---|---|
| NumPy arrays are general-purpose containers for data and can have any number of dimensions: 1-D, 2-D, 3-D, etc. | NumPy matrix is restricted to 2D data only, meaning it can only represent rows and columns. |
| It supports multi-dimensional arrays, which can hold complex datasets, including vectors, matrices, tensors, and more. | It is a specialized subclass of ndarray, but its functionality is much more limited compared to arrays. |
The number of dimensions is flexible and defined by the shape attribute. | All operations are performed on 2D structures; you cannot create a 3D matrix with np.matrix. |
import numpy as np
arr_3d = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]]) # 3-D shape array
print(arr_3d.shape) # Output: (2, 2, 2)
mat_2d = np.matrix([[1, 2], [3, 4]]) # 2-D shape matrix
print(mat_2d.shape) # Output: (2, 2)2. Operations (Element-wise vs Matrix-specific)
NumPy Array (ndarray) | NumPy Matrix (matrix) |
|---|---|
Element-wise operations are the default behavior for arrays. For example, the * operator performs element-wise multiplication (not matrix multiplication). | Matrix operations are the default behavior for matrices. The * operator performs matrix multiplication (not element-wise multiplication). |
For matrix multiplication, you need to use np.dot(), np.matmul(), or @ (in Python 3.5+) | For element-wise multiplication, you would need to use np.multiply() or np.multiply(arr1, arr2). The matrix class also overloads the @ operator to perform matrix multiplication. |
import numpy as np
arr1 = np.array([[1, 2], [3, 4]])
arr2 = np.array([[5, 6], [7, 8]])
print(arr1 * arr2) # Array Element-wise multiplication
# Output: [[ 5 12] [21 32]]
multiplication_result = np.dot(arr1, arr2) # Matrix multiplication using np.dot()
multiplication_result = arr1 @ arr2 # Or using the @ operator (Python 3.5+):
mat1 = np.matrix([[1, 2], [3, 4]])
mat2 = np.matrix([[5, 6], [7, 8]])
print(mat1 * mat2) # Matrix multiplication (not element-wise)
# Output => [[19 22] [43 50]]3. Shape and Return Type
NumPy Array (ndarray) | NumPy Matrix (matrix) |
|---|---|
| Return an array when performing most operations. | Return as a matrix (rather than an ndarray) when performing most operations. |
| Shape is flexible and can represent data with any number of dimensions. | Shape is always (n, m) for 2-D matrices. |
After a matrix operation like np.dot(), the return type will still be a NumPy array, not necessarily an array of type matrix. | When performing matrix operations like multiplication, the result is still of type matrix. |
import numpy as np
arr1 = np.array([[1, 2], [3, 4]])
arr2 = np.array([[5, 6], [7, 8]])
result = np.dot(arr1, arr2)
print(result.shape) # Output: (2, 2)
print(type(result)) # <class 'numpy.ndarray'>
mat1 = np.matrix([[1, 2], [3, 4]])
mat2 = np.matrix([[5, 6], [7, 8]])
result = mat1 * mat2
print(result.shape) # Output: (2, 2)
print(type(result)) # <class 'numpy.matrix'>4. Broadcasting
Broadcasting in NumPy allows arrays of different shapes to be combined and operated on together, automatically aligning them based on their dimensions. Arrays can be broadcasted across dimensions when performing operations. This is not possible with matrices, as they are limited to 2D.
Broadcasting does not apply to matrices in the same way as arrays. Matrices are strictly 2D, and if you try to perform operations on matrices with incompatible shapes, it will raise an error.
import numpy as np
arr1 = np.array([[1, 2], [3, 4]])
arr2 = np.array([5, 6])
print(arr1 + arr2) # Broadcasting: adds [5, 6] to each row of arr1
# Output => [[ 6 8] [ 8 10]]5. Interchangeability with Other Libraries
- Arrays are more commonly used in modern scientific computing and are compatible with many other libraries like
pandas,scikit-learn, andmatplotlib. Matrices are less common in most modern scientific applications and are typically used in legacy code or very specific cases where matrix operations are central (e.g., linear algebra). - The general-purpose nature of
ndarraymakes it versatile and suitable for various fields, such as machine learning, image processing, and numerical simulations. Many newer libraries (e.g.,pandas,scikit-learn) preferndarrayovermatrix, and using matrices might limit compatibility.
Conclusion
Understanding the basics of NumPy matrices is essential for efficient numerical computing in Python. We’ve explored the mathematical concept of a matrix, which serves as a fundamental structure in linear algebra, and how NumPy implements it for fast, array-based operations.
We also differentiated between NumPy arrays and matrices, highlighting their similarities and distinct characteristics. While both structures are useful, knowing when to use each can optimize performance and ease of implementation in various computational tasks. With this knowledge, you can now confidently leverage NumPy matrices for handling large datasets, performing matrix operations, and solving complex mathematical problems in Python.
Code snippets and programs related to Introduction to NumPy Matrix and NumPy Array vs NumPy Matrix, can be accessed from GitHub Repository. This GitHub repository all contains programs related to other topics in NumPy tutorial.
Related Topics
- Create Arrays with Predefined Values using np.zeros(), np.ones(), np.full() and np.empty()Create Arrays with Predefined Values NumPy library provides various functions to create arrays with predefined values. While creating an array, these NumPy functions helps to initialize the arrays with initial values. In last tutorial, we learned about Key Features of NumPy Arrays in Python. In this article, we will learn about 4 functions to create…
- Create Matrix in NumPy | Identity Matrix and Diagonal Matrix using numpy.eye() & numpy.diag() FunctionsA NumPy matrix is a 2-D array, a rectangular grid of numbers organized in rows and columns. In NumPy, the matrix class is a specialized 2-D ndarray object, and it enforces a stricter 2-D structure, meaning it only supports two-dimensional arrays. NumPy library provides additional methods specifically designed for matrix operations. In previous articles, we…
- Introduction to NumPy Matrix | NumPy Array vs NumPy MatrixNumPy (Numerical Python) is a popular Python library used for numerical and scientific computing. It provides a powerful N-dimensional array object called ndarray, which can be used to store and manipulate large datasets efficiently. While NumPy arrays are general-purpose containers for data, the concept of a matrix is often needed when performing operations related to…
- np.linspace(): Create Arrays with Evenly Spaced Numbers in NumPy (with Example Programs)NumPy is a powerful Python library for numerical computing, and np.linspace() is one of the most useful functions for generating arrays of evenly spaced values within a specified range. In previous tutorials, we learned about Key Features of NumPy Arrays in Python. This tutorial will provide a step-by-step guide to understand how to use np.linspace() effectively,…
- np.logspace(): Create Array of Evenly Spaced Numbers on Logarithmic Scale (with Example Programs)NumPy is a powerful Python library for numerical computing, and np.logspace() is one of the powerful function to create array of evenly spaced numbers on logarithmic scale. In previous tutorials, we learned about Key Features of NumPy Arrays in Python. This tutorial will provide a step-by-step guide to understand how to use np.logspace() effectively, with examples.…

Amazing forum posts Appreciate it!