NumPy (Numerical Python) is a powerful library for numerical computing in Python. It provides support for large multidimensional arrays and matrices, and it also provides a collection of mathematical functions to operate on these arrays. Understanding the attributes of NumPy arrays is essential for efficiently working with them.
In previous articles, we learned about NumPy Arrays and How to create NumPy Arrays using Lists or Tuples or using different methods like np.arange(), np.linspace() and np.logspace(). In this tutorial, we will go through the most important attributes of NumPy arrays, explain them with example programs.
NumPy Array Attributes
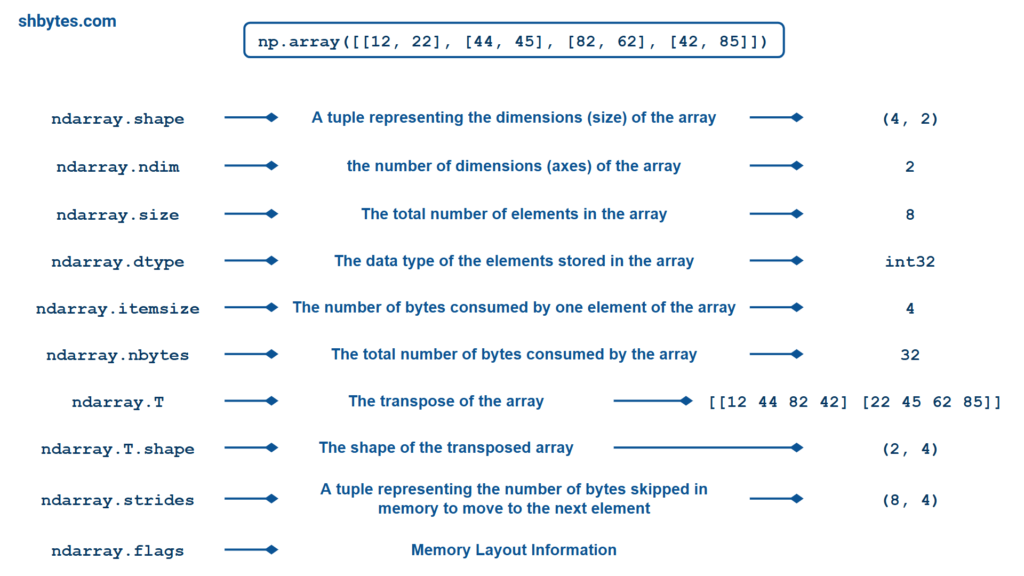
There are multiple array attributes that we can access after creating a NumPy array. These attributes are very useful to understand the overall structure of array and while performing mathematical operations on them.
ndarray.shape
The shape attribute returns a tuple representing the dimensions (size) of the array. The length of this tuple indicates the number of dimensions (axes) of the array, and each element in the tuple represents the size of the array along that dimension.
import numpy as np
array_6 = np.array([12, 22, 32, 44, 45, 56]) # 1-D array
print(array_6.shape) # Output => (6,)
array_4x2 = np.array([[12, 22], [44, 45], [82, 62], [42, 85]]) # 2-D array
print(array_4x2.shape) # Output => (4, 2)
array_2x2x2 = np.array([[[12, 22], [44, 45]], [[82, 62], [42, 85]]]) # 3-D array
print(array_2x2x2.shape) # Output => (2, 2, 2)- For a 1-D array,
shapewill return a tuple with one element. The arrayarray_6is a 1-D array and has 6 elements, so its shape is(6,). - For a 2D array,
shapewill return a tuple with two elements. The arrayarray_4x2is a 2-D array, so its shape is(4, 2). - For an n-dimensional array,
shapereturns a tuple with n elements. The arrayarray_2x2x2is a 3-D array, so its shape is(2, 2, 2).
ndarray.ndim
The ndim attribute gives the number of dimensions (axes) of the array. 0-D (zero dimensional) array is called as scalar.
import numpy as np
array_1 = np.array([12, 22, 32, 44, 45, 56]) # 1-D array
print(array_1.ndim) # Output => 1
array_2 = np.array([[12, 22], [44, 45], [82, 62], [42, 85]]) # 2-D array
print(array_2.ndim) # Output => 2
array_3 = np.array([[[12, 22], [44, 45]], [[82, 62], [42, 85]]]) # 3-D array
print(array_3.ndim) # Output => 3- Scalar (0-D array) has
ndim = 0. - 1-D array has
ndim = 1. The arrayarray_1is a 1-D array, soarray_1.ndimreturns1. - 2-D array has
ndim = 2, and so on. The arrayarray_2is a 2-D array, soarray_2.ndimreturns2. - n-D array has
ndim = n, and so on. The arrayarray_3is a 3-D array, soarray_3.ndimreturns3.
ndarray.size
The size attribute returns the total number of elements in the array. It is equal to the product of the elements in the shape of the array.
import numpy as np
array_6 = np.array([12, 22, 32, 44, 45, 56]) # 1-D array
print(array_6.size) # Output => 6
array_10 = np.array([[12, 22], [44, 45], [82, 62], [42, 85], [78, 85]]) # 2-D array
print(array_10.size) # Output => 10
array_8 = np.array([[[12, 22], [44, 45]], [[82, 62], [42, 85]]]) # 3-D array
print(array_8.size) # Output => 8sizecan be used to get the total number of elements in any array, regardless of its dimensions. It is computed as the product of the dimensions of the array.array_6is a 1-D array and has 6 elements, so itssizeis6.array_10is a 2-D array and has 10 elements, so itssizeis10.array_8is a 3-D array and has 8 elements, so itssizeis8.
ndarray.shape vs. ndarray.size
While shape gives the dimensions (rows, columns) of the array, size tells you the total number of elements in the array.
import numpy as np
array_5x2 = np.array([[12, 22], [44, 45], [82, 62], [42, 85], [78, 85]]) # 2-D array
print(array_5x2.shape) # Output: (5, 2)
print(array_5x2.size) # Output => 10
array_2x2x2 = np.array([[[12, 22], [44, 45]], [[82, 62], [42, 85]]]) # 3-D array
print(array_2x2x2.shape) # Output: (2, 2, 2)
print(array_2x2x2.size) # Output => 8array_5x2is a 2-D array,shapegives(5, 2), meaning 5 rows and 2 columns, whilesizegives the total number of elements, which is10.array_2x2x2is a 3-D array,shapegives(2, 2, 2), whilesizegives the total number of elements, which is8.
ndarray.dtype
The dtype attribute returns the data type of the elements stored in the array. NumPy arrays can have elements of different data types such as int32, float64, complex128, etc. The dtype attribute is useful for checking the type of data stored in the array and for ensuring data consistency when performing operations.
import numpy as np
array_int = np.array([12, 22, 32, 44, 45, 56]) # 1-D array
print(array_int.dtype) # Output => int32
array_float = np.array([[12.23, 22.3], [44.6, 45.7], [82.9, 62.2], [42, 85]]) # 2-D array
print(array_float.dtype) # Output => float64
array_complex = np.array([[[1+2j, 2+1j]], [[5+4j, 6+4j]]]) # 3-D array
print(array_complex.dtype) # Output => complex128array_intarray contains integer numbers anddtypewill returnint32.array_floatarray contains float numbers anddtypewill returnfloat64.array_complexarray contains complex numbers anddtypewill returncomplex128.
ndarray.itemsize
The itemsize attribute returns the number of bytes consumed by one element of the array. The itemsize attribute is useful for understanding the memory usage of the array. It is the size in bytes of each element in the array, based on its data type.
import numpy as np
array_int = np.array([12, 22, 32, 44, 45, 56]) # 1-D array
print(array_int.itemsize) # Output => 4
array_float = np.array([[12.23, 22.3], [44.6, 45.7], [82.9, 62.2], [42, 85]]) # 2-D array
print(array_float.itemsize) # Output => 8
array_complex = np.array([[[1+2j, 2+1j]], [[5+4j, 6+4j]]]) # 3-D array
print(array_complex.itemsize) # Output => 16- The array
array_intconsists ofint32values, which typically use 4 bytes in memory. Itsitemsizewill be4. - The array
array_floatconsists offloat64values, which typically use 8 bytes in memory. Itsitemsizewill be8. - The array
array_complexconsists ofcomplex128values, which typically use 16 bytes in memory. Itsitemsizewill be16.
ndarray.nbytes
The nbytes attribute returns the total number of bytes consumed by the array. It is equivalent to itemsize * size. nbytes gives you the total memory usage of the array, which is useful for managing large datasets in memory.
import numpy as np
array_int = np.array([12, 22, 32, 44, 45, 56]) # 1-D array
print(array_int.nbytes) # Output => 24 (4 x 6)
array_float = np.array([[12.23, 22.3], [44.6, 45.7], [82.9, 62.2], [42, 85]]) # 2-D array
print(array_float.nbytes) # Output => 64 (8 x 8)
array_complex = np.array([[[1+2j, 2+1j]], [[5+4j, 6+4j]]]) # 3-D array
print(array_complex.nbytes) # Output => 64 (16 x 4)- The array
array_inthas 6 elements, and each element is of typeint32, which consumes 4 bytes. Therefore, the total memory usage is4 x 6 => 24bytes. - The array
array_floathas 8 elements, and each element is of typefloat648 x 8 => 64bytes. - The array
array_complexhas 4 elements, and each element is of typecomplex64, which consumes 16 bytes. Therefore, the total memory usage is16 x 4 => 64bytes.
ndarray.T – Transpose of Array
The T attribute returns the transpose of the array. It swaps the rows and columns of the array (for 2-D arrays) or more generally, swaps the axes of the array. The T attribute works for arrays of any dimension, though it is most commonly used for 2-D arrays. For higher-dimensional arrays, it reverses the order of axes.
import numpy as np
array_6 = np.array([12, 22, 32, 44, 45, 56]) # 1-D array
print(array_6.T) # Output: [12 22 32 44 45 56]
array_4x2 = np.array([[12, 22], [44, 45], [82, 62], [42, 85]]) # 2-D array
print(array_4x2.T)
# [[12 44 82 42]
# [22 45 62 85]]
print(array_4x2.T.shape) # Output => (2, 4)
array_3x2x1 = np.array([[[12], [44]], [[82], [42]], [[22], [72]]]) # 3-D array
print(array_3x2x1.T)
# [[[12 82 22]
# [44 42 72]]]
print(array_3x2x1.T.shape) # Output => (1, 2, 3)array_6is a 1-D array with shape(6,)andarray_6.Ttranspose of this array shows no change in the shape.array_4x2is a 2-D array with shape(4, 2). Witharray_4x2.Tthe array is transposed, meaning its rows and columns are swapped. Shape of the transposed array is(2, 4).array_3x2x1is a 3-D array with shape(3, 2, 1). Witharray_3x2x1.Tthe array is transposed, meaning it will reverse the order of axes. Shape of the transposed array is(1, 2, 3).
ndarray.real and ndarray.imag
The real and imag attributes return the real and imaginary parts of the array, respectively. These are used for complex-valued arrays. These attributes are only meaningful for arrays of complex numbers.
import numpy as np
array_complex_1d = np.array([1+2j, 2+1j]) # 1-D array
print(array_complex_1d.real) # Output => [1. 2.]
print(array_complex_1d.imag) # Output => [2. 1.]
array_complex_2d = np.array([[1+2j, 2+1j], [5+4j, 6+4j]]) # 2-D array
print(array_complex_2d.real) # Output => [[1. 2.] [5. 6.]]
print(array_complex_2d.imag) # Output => [[2. 1.] [4. 4.]]
array_complex_3d = np.array([[[1+2j, 2+1j]], [[5+4j, 6+4j]]]) # 3-D array
print(array_complex_3d.real) # Output => [[[1. 2.]] [[5. 6.]]]
print(array_complex_3d.imag) # Output => [[[2. 1.]] [[4. 4.]]]- The 1-D array
array_complex_1dcontains complex numbers, sorealandimagextract the real and imaginary parts as 1-D array only.array_complex_1d.real=>[1. 2.];array_complex_1d.imag=>[2. 1.]; - The 2-D array
array_complex_2dcontains complex numbers.realandimagattribute will extract the real and imaginary parts as 2-D array.array_complex_2d.real=>[[1. 2.] [5. 6.]];array_complex_2d.imag=>[[2. 1.] [4. 4.]]; - The 3-D array
array_complex_3dcontains complex numbers.array_complex_3d.realandarray_complex_3d.imagwill extract the real and imaginary parts as 3-D array.
ndarray.strides
The strides attribute returns a tuple representing the number of bytes that must be skipped in memory to move to the next element along each dimension. strides is particularly useful for advanced manipulation of memory layouts and optimization of memory access patterns.
import numpy as np
array_6 = np.array([12, 22, 32, 44, 45, 56]) # 1-D array
print(array_6.strides) # Output => (4,)
array_4x2 = np.array([[12, 22], [44, 45], [82, 62], [42, 85]]) # 2-D array
print(array_4x2.strides) # Output => (8, 4)
array_3x2x1 = np.array([[[12], [44]], [[82], [42]], [[22], [72]]]) # 3-D array
print(array_3x2x1.strides) # Output => (8, 4, 4)array_6is a 1-D array having 6 elements. The stride of 4 bytes corresponds to moving to the next element.array_4x2is a 2-D array having 4 rows and 2 columns.array_4x2.strides=>(8, 4), the stride of 8 bytes corresponds to moving to the next row, and 4 bytes corresponds to moving to the next column.array_3x2x1is a 3-D array having 3 rows, 2 columns and 1 depth.array_3x2x1.strides=>(8, 4, 4), the stride of 8 bytes corresponds to moving to the next row, 4 bytes corresponds to moving to the next column and 4 bytes correspond to moving to the next depth.
ndarray.flags
The flags attribute returns a dictionary-like object that provides information about the memory layout of the array, such as whether it is contiguous in memory, if it is a write-able array, etc.
import numpy as np
array_4x2 = np.array([[12, 22], [44, 45], [82, 62], [42, 85]]) # 2-D array
print(array_4x2.flags)
# C_CONTIGUOUS : True
# F_CONTIGUOUS : False
# OWNDATA : True
# WRITEABLE : True
# ALIGNED : True
# WRITEBACKIFCOPY : FalseC_CONTIGUOUSindicates whether the array is stored in a contiguous block of memory in row-major order.WRITEABLEindicates whether the array is writeable.ALIGNEDindicates whether the memory is aligned for efficient access.
Conclusion
Understanding the various attributes of NumPy arrays is essential for efficiently working with multi-dimensional data in Python. In this tutorial, we explored NumPy array attributes. Mastery of these attributes can significantly enhance your ability to manipulate, optimize, and understand NumPy arrays, ultimately making your data analysis and scientific computing tasks more efficient and manageable.
Code snippets and programs related to NumPy Array Attributes and topics covered in this tutorial, can be accessed from GitHub Repository. This GitHub repository all contains programs related to other topics in NumPy tutorial.
Related Topics
- numpy.array(): Create NumPy Arrays using Lists, Tuples and Arrays (with Example Programs)NumPy (Numerical Python) is one of the most powerful libraries for numerical computations, data manipulation, and analysis in Python. At the core of NumPy is the ndarray, a multi-dimensional or N-dimensional array that allows to store and manipulate large datasets efficiently. NumPy provides several ways to create arrays, from simple ones to more complex multi-dimensional…
- numpy.arange(): Create Array of Evenly Spaced Numbers within a Range (with Example Programs)NumPy library provides various functions to create arrays with evenly spaced numbers within range. In previous tutorials, we learned about Key Features of NumPy Arrays in Python. In this tutorial, we will learn to create NumPy arrays using numpy.arrange() function. numpy.arange() to Create Array of Evenly Spaced Numbers within a Range numpy.arange() is used to create…
- NumPy Array in Python: First Step into Numerical PythonNumPy array in Python are basic entities for numerical computations. They originate from the NumPy library, an essential package in Python for scientific computing. A NumPy array also termed as ndarray, is highly efficient and an object of multi-dimensional array (N-dimensional array), which provides the base functions of numerical operations. Being NumPy Arrays an essential…
- NumPy Array Attributes | ndarray Attributes (with Example Programs)NumPy (Numerical Python) is a powerful library for numerical computing in Python. It provides support for large multidimensional arrays and matrices, and it also provides a collection of mathematical functions to operate on these arrays. Understanding the attributes of NumPy arrays is essential for efficiently working with them. In previous articles, we learned about NumPy…
- np.logspace(): Create Array of Evenly Spaced Numbers on Logarithmic Scale (with Example Programs)NumPy is a powerful Python library for numerical computing, and np.logspace() is one of the powerful function to create array of evenly spaced numbers on logarithmic scale. In previous tutorials, we learned about Key Features of NumPy Arrays in Python. This tutorial will provide a step-by-step guide to understand how to use np.logspace() effectively, with examples.…

This is nicely expressed. !
Useful content, Thanks a lot!